|
Функция числа предков с учетом редукции
Для того чтобы найти число предков в поколении с учетом редукции, необходимо найти сумму числа предков в каждой возрастной группе с учетом редукции. Число предков в возрастной группе с учетом редукции можно определить как разность между числом предков без учета редукции и суммой редукций возникающих за счет персон в текущем поколении и с учетом персон предыдущих поколений:
q=Q-(f(Q)+F(Q,Qn-1)), где (1)
Q - число предков в рассматриваемой возрастной группе поколения n из числа предков (Y) одной возрастной группы общества до наступления редукции,
Qn-1 – сумма числа предков данной возрастной группы в предыдущих n-1 поколениях,
f(Q) - среднее число предков (одной возрастной группы), на которое происходит уменьшение в текущем поколении восходящего родословного дерева с учетом редукции только в этом поколении,
F(Q,Qn-1) - функция, учитывающая редукцию между персонами текущего поколения восходящего родословного дерева и предыдущими поколениями.
Найдем каждое из этих слагаемых.
Число предков в возрастной группе восходящего родословного дерева без учета редукции определяется в соответствии с Законом о числе предков восходящего родословного дерева в возрастных группах без учета редукции (Qni=Q=Q(n-1)(i-1)+Q(n-1)(i)).
Теперь найдем насколько предков уменьшится восходящее родословное дерево, если из возрастной группы общества (с периодом равным разнице в возрасте родителей), состоящей из Y персон (Y=Yобщ/Vср×(Vo-Vм), где Yобщ ‑ общая численность населения популяции, Vср ‑ средний возраст жизни, Vo,Vм – средний возраст отца и матери), в восходящее родословное дерево попало Q человек (это первое слагаемое f(Q) в формуле 1).
Рассмотрим общество за некоторый период времени с постоянными условиями. Найдем в нем средний возраст отца (Vo) и матери(Vм). Разделим общество на возрастные группы по V=(Vo-Vм) лет, в которых все персоны будем считать одного возраста.
Рассмотрим одну возрастную группу в обществе из S семей (S отцов и S матерей). Будем рассматривать семьи со средним числом детей равным целому значению. Самый простой и удобный вариант, если среднее число детей в каждой семье равно целому числу, например, двум. Если среднее число детей в семье является дробным числом-dср, то можно рассматривать семьи с числом детей равным целому от dср ( d0=|dср|) и наибольшему целому (d1=|dср|+1=d0+1). Обозначим через Sd число семей со средним числом детей равным d. Тогда, S=Sd0+Sd1.
И учитывая, что
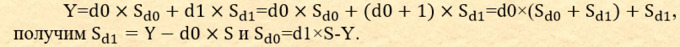
Или можно рассматривать семьи с конкретными числами детей, тогда 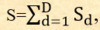 , где , где
D - максимальное число детей в семье.
Для дробного значения числа детей в семье D=d1.
Например, в 5 (S) семьях со средним числом детей равным 2,4 (dср, следовательно D=3, d0=2, d1=3) и состоящих из 3 (S2) семей с двумя детьми и 2 (S3) семей с тремя детьми имеется 12 детей (5×2,4 или 3х2+2х3).
Тогда всего детей будет dсрхS=Y, у каждого из которых будет один теоретический отец без учета редукции (всего Y, а с учетом редукции S).
|
Закон о числе фактических и теоретических предков в перспективе. В перспективе для всех детей (из S семей общества), попавших в восходящее родословное дерево, в поколении родителей будет S фактических отцов(матерей) и Y теоретических (без учета редукции) отцов(матерей), где
Y=dср х S,
dср - среднее число детей в семье. |
|
Закон о редукции в семье. В перспективе в каждой семье на d детей (братьев и сестер) приходится уменьшение на (d-1) персону (для отцов и матерей соответственно) в поколении родителей, а для всех S семей на (dср - 1)хS, где
dср- среднее число детей в семье.
|






Рассмотрим пример. Предположим из возрастной группы в 10 (Y) человек со средним числом детей равным 2,5 (две семьи с двумя детьми (S2=2, i=2, d=2) и две семьи с тремя детьми (S3=2, i=2, i=3, d=3). в родословное дерево попали все 10 человек. Следовательно, число родителей до наступления редукции равно Y, после редукции S=10/2,5=4.
Пронумеруем всех детей в семьях: 12 34 567 890
Если в восходящее родословное дерево попадет 2 человека, то наступление редукции маловероятно, если 4 – то есть вероятность, что редукции не будет (по одному ребенку из каждой семьи), а если более 4 - то редукция наступит обязательно.
Предположим в восходящее родословное дерево попало 8 (Q) персон.
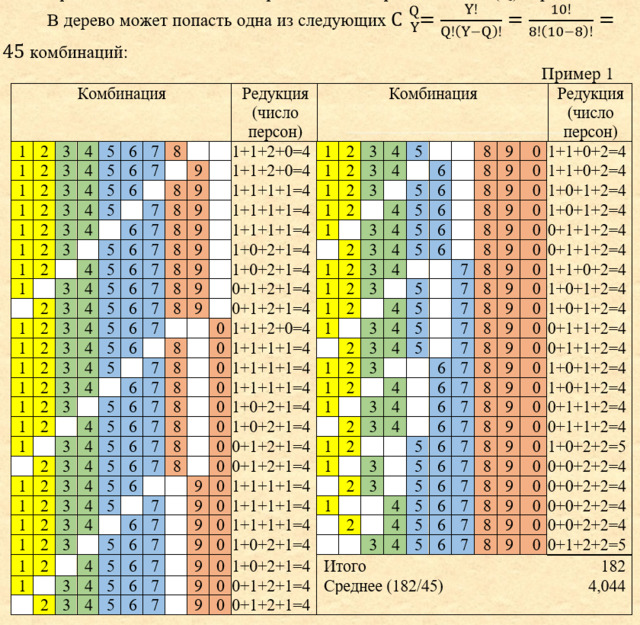

|
Закон о числе повторений предков в одной возрастной группе.
 |
Введем понятие коэффициента редукции:
|
Определение коэффициента редукции. Количество попарных комбинаций (возможных совпадений) персон, на которых приходится одно совпадение предков (уменьшения на одного предка в постоянных условиях, для лиц одного пола и возраста) будем называть коэффициентом редукции (P).
|
Следовательно, при среднем числе детей равным 2 коэффициент редукции является постоянным P=(Y-1), а при среднем числе детей равным трем 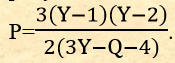 . .
Наиболее удобно использование коэффициента редукции при среднем числе детей равным 2, поскольку в этом случае он зависит только от одной переменной.
Как говорилось ранее, можно искать как число предков в поколении, так и общее число предков во всех поколениях.
|
Закон об общем числе предков. Общее число предков восходящего родословного дерева до текущего поколения n является суммой числа предков в возрастных группах, определяемых формулой:
qn= Qn-f(Qn), где
Qn - общее число предков (без учета редукции) одной возрастной группы c учетом всех поколений до текущего поколения, из числа предков (Y) одной возрастной группы общества, которое можно выразить формулой:
Qn=Q+Qn-1,
Q - число предков в рассматриваемой возрастной группе поколения n из числа предков (Qn) одной возрастной группы общества (Y) и определяется в соответствии с Законом о числе предков восходящего родословного дерева в возрастных группах без учета редукции,
Qn-1 – сумма числа предков данной возрастной группы в предыдущих n-1 поколениях до наступления редукции,
f(Qn) - cреднее число предков (одной возрастной группы), на которое происходит уменьшение во всех поколениях восходящего родословного дерева, которое можно выразить формулой:
f(Qn)= f(Q+ Qn-1)= f(Q)+f(Qn-1)+F(Q,Qn-1)
Откуда F(Q, Qn-1)= f(Qn)-(f(Q)+f(Qn-1)), где
f(Q) ‑  cреднее число предков (одной возрастной группы), на которое происходит уменьшение (число повторений предков) в текущем поколении восходящего родословного дерева с учетом редукции только в этом поколении, значения которой можно определить из Закона о числе повторений предков в одной возрастной группе, cреднее число предков (одной возрастной группы), на которое происходит уменьшение (число повторений предков) в текущем поколении восходящего родословного дерева с учетом редукции только в этом поколении, значения которой можно определить из Закона о числе повторений предков в одной возрастной группе,
f(Qn-1) - cреднее число предков (одной возрастной группы), на которое происходит уменьшение (число повторений предков) во всех предыдущих поколениях восходящего родословного дерева.
F(Q,Qn-1) - функция, учитывающая редукцию между персонами текущего поколения восходящего родословного дерева и предыдущими поколениями.
Значения функции f(Qn) можно определить из Закона о числе повторений предков в одной возрастной группе,
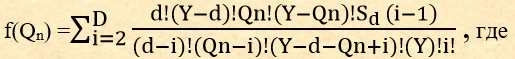
d-число детей в семье,
Sd -число семей из числа Y с числом детей равным d ≥ 2,
D‑ максимальное число детей в семье.
Для среднего числа детей равного двум:
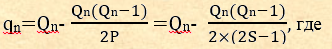
Р - коэффициент редукции,
S – число предков одной возрастной группы общества (с учетом редукции), число семей.
|
Найдем число персон с учетом редукции между персонами текущего поколения восходящего родословного дерева и предыдущими поколениями для среднего числа детей равного 2 и 3. Это третье слагаемое F(Q,Qn-1) в формуле 1.
Обозначим: a=Q, b=Qn-1, тогда Qn= Q+Qn-1=a+b

В соответствии с формулой 1 общая формула для расчета числа предков в одной возрастной группе с учетом редукции будет выглядеть так:
|
Первый закон редукции предков. Закон о числе предков в поколении (возрастной группе) с учетом редукции. Число предков в поколении восходящего родословного дерева является суммой числа предков в возрастных группах этого поколения, определяемых формулой
q= Q-f(Q)-F(Q,Qn-1) , где
Q - аналогично Закону об общем числе предков,
Qn-1 – аналогично Закону об общем числе предков,
f(Q) ‑ аналогично Закону об общем числе предков,
F(Q,Qn-1) - функция, учитывающая редукцию между персонами текущего поколения восходящего родословного дерева и предыдущими поколениями, значения которой можно определить из Закона об общем числе предков и его следствия.
Для среднего числа детей равного двум:
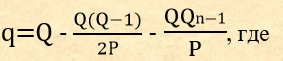
Р - коэффициент редукции.
|
Первое вычитаемое равно количеству повторений предков внутри только одного поколения, а второе-с учетом всех предыдущих поколений.
Полученное значение является одним из исходных слагаемых для числа предков в следующем поколении без учета редукции. (см. Закон о числе предков восходящего родословного дерева в возрастных группах без учета редукции.)
Рассмотрим пример для среднего числа детей равного 2. Рассмотрим группу общества из 8 человек (допустим, мужчин) со средним числом детей равным 2-м (всего 16 детей, у которых без учета редукции-16 отцов, а редукция составит 8 человек). Коэффициент редукции P=15. Если в возрастную группу восходящего родословного дерева попали все 16 человек, то количество повторений предков в поколении будет равно: (Q×(Q 1)/2)/Р=16×15/2/15=8.
А если в возрастную группу одного поколения попало только 6 человек, то произойдет только (Q×(Q-1)/2)/Р=6×5/2/15=1 повторение предков. И, например, в следующее поколение попало 10 человек, тогда в нем произойдет уменьшение на ((Q×(Q-1)/2)+Q×Qn-1)/Р = (10×9/2+10×6))/15=105/15=7 предков с учетом предков двух поколений. Три из которых произошли за счет пересечений внутри поколения и четыре за счет пересечения с персонами предыдущего поколения. Таким образом, в родословном дереве произошло уменьшение на 8 персон (7+1), также, как и в обществе.
Рассмотрим другой пример, с учетом возраста родителей. Для наглядности, и удобства расчетов разместим данные соответствующие треугольнику Паскаля, аналогичные Таблице 2 (с учетом редукции и с учетом округления) на временной шкале (для отслеживания одинаковых возрастных групп в разных поколениях, в которых может произойти редукция при наличии достаточного числа предков), но с коэффициентом редукции равным 45 и средним возраст матери равным 25 годам, а отца 30 годам.
Таблица 5
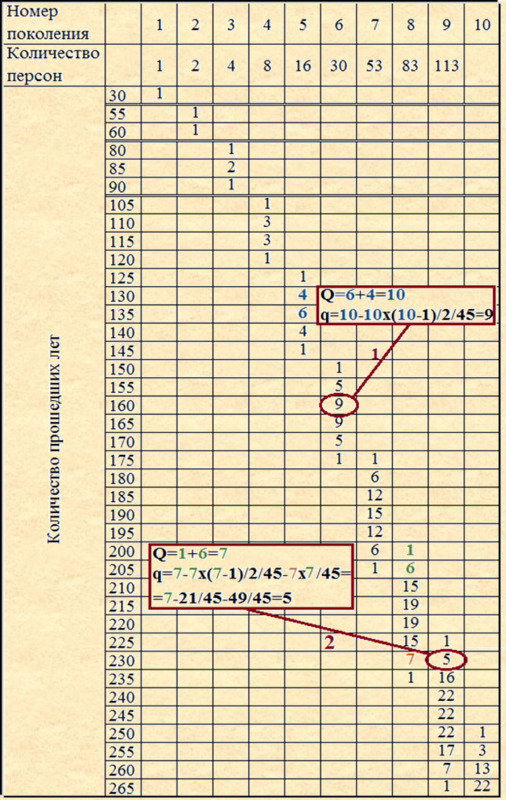
Из таблицы видно, что для данных условий в первых пяти поколениях редукции предков нет, но начиная с 6 поколения (160 лет тому назад) происходит редукция внутри одного поколения для двух возрастных групп. В этом случае (обозначено 1) в соответствии с Первым законом редукции предков происходит уменьшение на одного предка в двух возрастных группах.
Начиная с 7 поколения, 175 лет назад появляются одинаковые возрастные группы в разных поколениях восходящего родословного дерева, и таким образом в дополнение к возможной редукции внутри одного поколения появляется вероятность редукции в одной возрастной группе за счет разных поколений.
|
Закон о редукции в разных поколениях дерева. Редукция между персонами разных поколений восходящего родословного дерева происходит за счет разницы в возрасте между родителями.
|
Так, для данного примера в 9 поколении (230 лет тому назад) должно быть 7 персон, но с учетом 7 персон в предыдущем поколении в той же возрастной группе и в соответствии с Первым законом редукции предков число предков с учетом коэффициента редукции равного P=45, получим число предков, уменьшенное на два (обозначено 2).
То же значение можно получить с использованием Второго закона редукции предков. Общее число предков в возрастной группе равно Qn=7+7=14. Число предков в предыдущих поколениях равно Qn-1=7.
Тогда f(Qn) =14х(14-1)/2/45=2,022,
f(Qn-1)=(7x(7-1)/2)/45=0,467
q=Q-((Qn(Qn-1)-Qn-1(Qn-1-1))/2P =Q - f(Qn)+f(Qn-1)=7-2,022+0,467≈5
Заметим, что уменьшение числа предков за счет повторений между персонами разных поколений происходит не в самой младшей возрастной группе, а в возрастных группах, образующих максимальное число попарных комбинаций.
Учитывая, что в начальных поколениях (в связи с небольшим объемом статистических данных) могут быть значительные отклонения от среднего возраста отца и матери, вероятность повторения персон в разных поколениях восходящего родословного дерева несколько увеличивается.
Рассмотрим пример.
Объединив формулы q=Q - f(Q)-F(Q,Qn-1) f(Qn)=f(Q)+f(Qn-1)+F(Q,Qn-1)
(или f(Qn)-f(Qn-1)=f(Q)+F(Q,Qn-1)), получим:
|
Второй закон редукции предков. Закон о числе предков в поколении (возрастной группе) с учетом редукции. Число предков в поколении восходящего родословного дерева является суммой числа предков в возрастных группах этого поколения, определяемых формулой
q=Q - f(Qn)-f(Qn-1), где
Q - аналогично Закону об общем числе предков,
Qn - аналогично Закону об общем числе предков,
Qn-1 – аналогично Закону об общем числе предков,
f(Qn) - cреднее число предков (одной возрастной группы), на которое происходит уменьшение во всех поколениях восходящего родословного дерева (f(Qn)=f(Q)+f(Qn-1)+F(Q,Qn-1) или f(Qn)-f(Qn-1)=f(Q)+F(Q,Qn-1)),
f(Qn-1) - аналогично Закону об общем числе предков,
f(Q) ‑ аналогично Закону об общем числе предков,
F(Q,Qn-1) - функция, учитывающая редукцию между персонами текущего поколения восходящего родословного дерева и предыдущими поколениями, значения которой можно определить из Закона об общем числе предков и его следствия.
Для среднего числа детей равного двум:
q=Q-((Qn(Qn-1)-Qn-1(Qn-1-1))/2P, где
P - коэффициент редукции
|
Т.е. мы из числа предков без учета редукции (Q) вычитаем разность между числом повторений предков внутри всех поколений возрастной группы f(Qn) и числом повторений предков внутри всех предыдущих поколений возрастной группы f(Qn-1). и числом повторений предков внутри всех предыдущих поколений возрастной группы f(Qn-1).
|




