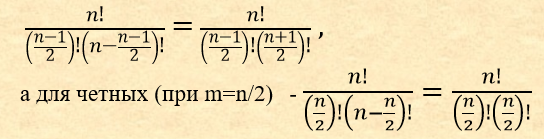|
Свойства функции числа предков с учетом редукции Все дальнейшие исследования расчеты и исследования будут проводиться исходя из демографической модели стационарного населения со средним числом детей равным двум. При необходимости расчетов для числа детей отличного от двух, необходимо учесть пропорциональное изменение численности населения для соответствующего поколения. Построим график с использованием полученных формул. Число предков в одном поколении восходящего родословного дерева с учетом редукции восходящего родословного дерева при постоянных значениях возраста отца (Vо=33) и возраста матери (Vм=28) в зависимости от коэффициента редукции (99,149 и 199) представлены ниже на графике. График 2 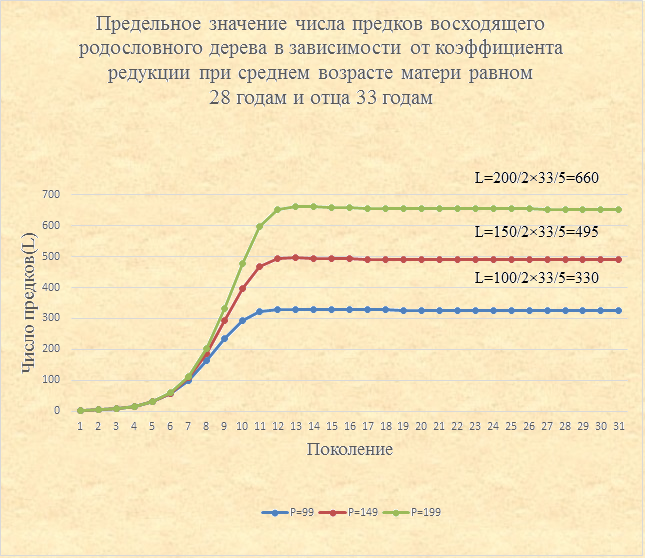
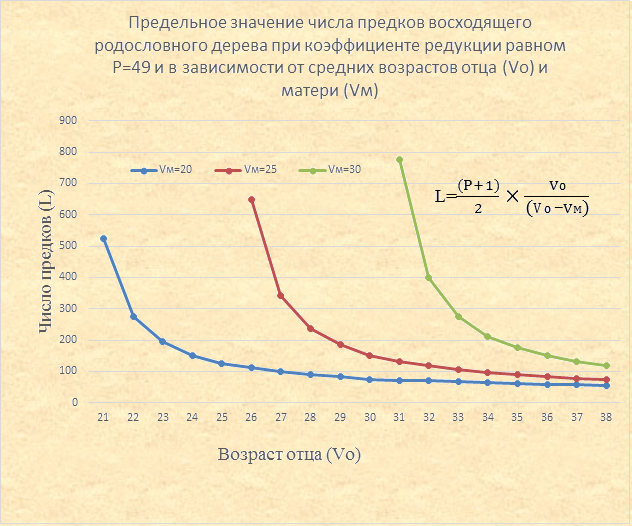
Смысл формулы можно разъяснить следующими рассуждениями. S ‑ число предков одной возрастной группы общества за период (Vo-Vм), а таких периодов Vo/(Vo-Vм). Теперь нам известен вид графика числа предков восходящего родословного дерева и параметры от которых он зависит (от численности населения, среднего числа детей в семье, среднего возраста отца и матери, теоретического числа предков в поколении дерева). Разумеется, что на практике число предков в каждом поколении не может быть постоянной величиной и будет иметь какой-то разброс, внутри диапазона близкого к этой величине. Из формулы видно, что предельное число предков в поколении восходящего родословного дерева уменьшается: - с уменьшением коэффициента редукции; - с увеличением среднего возраста отца; - с уменьшением среднего возраста матери. Ниже представлены графики предельных значений числа предков одного поколения восходящего родословного дерева с учетом редукции в зависимости от средних возрастов матери и отца. График 3
Тогда предельное значение числа предков (L), например, для среднего возраста матери (Vм) равного 28 лет и отца (Vo) -33 года, при коэффициенте редукции равном P=49, L=0,5×(P+1)×Vо/(Vо-Vм) =0,5 × 50 × 33 / (33-28) = 165 человек.
На графике ниже представлено предельное значение количества возрастных групп в зависимости от возраста отца, матери и коэффициента редукции. График 4 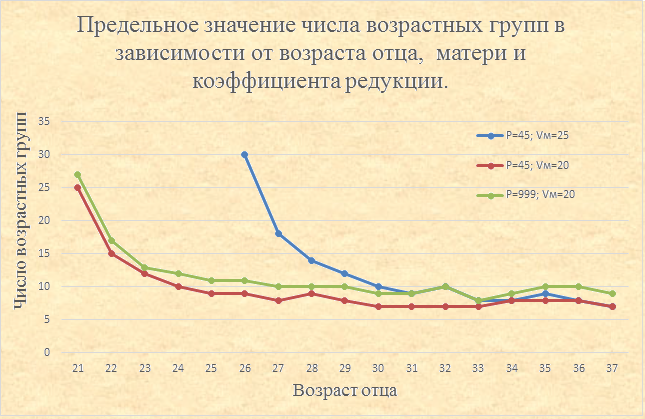
Исследования подтверждают следующую закономерность, которая следует из Закона постоянства числа предков.
Формулу L=Qlim × Vo/(Vo-Vм) можно объяснить следующим образом. Рождение любого ребенка происходит за период в среднем равный Vo. Число предков в возрастной группе за период равный разнице возраста родителей равно Qlim. А за весь период равный Vo, число предков будет равно Qlim×Vo/(Vo-Vм). Все персоны общества репродуктивного возраста должны распределиться по годам рассматриваемого периода (Vo), в следующем периоде будет следующее поколение общества. Эти предки, рожденные за период, равный возрасту отца, распределены по разным поколениям восходящего дерева в соответствии с Законом о связи поколений дерева и поколений общества. Другими словами, если у нас средний возраст отца равен 33 годам, то в перспективе в каждом поколении будет L предков (с учетом редукции) и за каждые 33 года в дереве будет присутствовать L предков, но во всех поколениях. Поскольку число персон в возрастной группе общества (Y) определить на практике не просто, рассмотрим коэффициент редукции на основе анализа восходящего родословного дерева. Предположим, что в одном поколении восходящего родословного дерева одной возрастной группы из 20 персон одного пола произошло уменьшение на 2‑х персон, т.е. две пары предков совпали. Это уменьшение является отражением различных условий в поколениях общества (общее количество населения, среднее числа детей, национальность, вероисповедание и пр.). Вообще из 20 персон (Q) можно составить 190 различных пар (число сочетаний из 20 по 2, Если же коэффициент редукции принять P=190, тогда уменьшение произойдет на одного предка. Исследовав несколько возрастных групп можно найти среднее значение коэффициента редукции для всего дерева (или его ветви). Чем больше таких возрастных групп будет исследовано, тем точнее найденное значение коэффициента редукции. Поскольку мы рассматриваем усредненное дерево для постоянных условий, то коэффициент редукции будет одинаковым (для среднего числа детей равного двум) для любых возрастных групп, как для Вас, так и для Вашего отца, деда и т.д. Конечно могут быть и исключения. Например, для многих персон дерева первая редукция появляется в среднем 7 поколении, а у одной персоны в 3 поколении. Если рассматривать много поколений, то вклад этого исключения минимизируется. Но для небольшого количества поколений это исключение лучше не учитывать. Вероятно, для других деревьев той же местности коэффициент редукции будет примерно таким же, а для другого времени, местности, пола (других постоянных условий) может измениться.
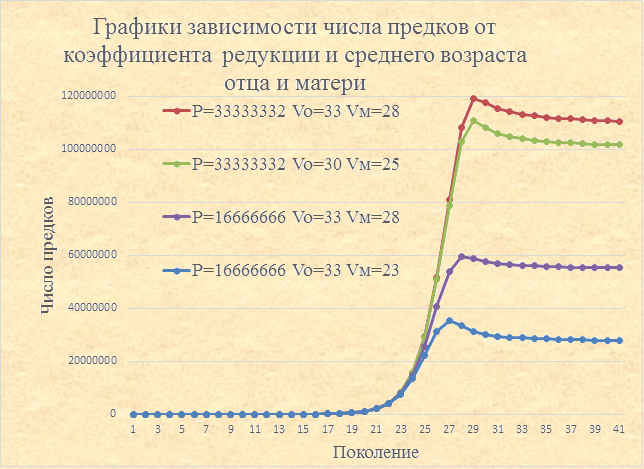
На основе результатов данного исследования определим, как давно жил наш ближайший общий предок. Это во многом зависит от компактности проживания наших предков. Но предполагая отсутствие каких-либо ограничений (в том числе на свободное передвижение наших предков, заключение браков и пр.), найдем ближайшее теоретически возможное время существования общего предка. Существование общего предка возможно при условии попадания всего населения Земли в наше усредненное родословное дерево. Предположим это было 30 поколений назад (в соответствии с вышеприведенным примером), когда на Земле проживало около 500 миллионов человек, одного пола - 250 миллионов. Если они все были предками любого из нас, то у нас был и общий предок. Уменьшим это значение на 20% (до 200 миллионов) с учетом того, что точная численность не известна, часть населения была бездетна, погибла в войнах и от болезней и прочее. Предположим, что средняя продолжительность жизни равна 60 лет. Следовательно, ежегодно рождалось и умирало 3333333 (200000000/60) человека, а число предков в одном поколении при среднем возрасте отца равном 33 годам в перспективе равно Найдем коэффициент редукции из Закона постоянства числа предков. График 5
Таким образом, для данных параметров, с учетом необходимости попадания в поколение дерева всех персон поколения общества репродуктивного возраста, общий предок возможен не ранее 32 поколения (хотя требуемое количество предков в 110 млн. будет достигнуто уже в 28 поколении, но за счет персон из других поколений общества). Для других параметров, как видно на графиках, это значение может измениться в несколько раз. Как видно на графике, после достижения небольшого максимума (при других параметрах он может отсутствовать), в каждом поколении число предков превышает общее число населения (за счет других поколений общества), постепенно стремясь к нему. Но с учетом того, что общая численность населения в более ранние годы была меньше, то и график будет иметь тенденцию к уменьшению. Этот график носит бесспорно теоретический характер, а в действительности же безусловно существовали различного рода ограничения, о которых речь шла выше, и которые отодвигали эту границу, а в некоторых случаях и вовсе не позволяли ее достичь, достигая лишь локальной численности населения конкретной местности. Максимальное значение может быть найдено по приближенной формуле: ((0,095×(Vо-Vм)-0,2)×(lg(P+1)-1)+Vо/2)/(Vо-Vм)×(Р+1). Например, для вышеуказанных характеристик (Vо=33, Vм=28, P=33333332) ошибка между расчетным значением максимального значения и смоделированного составит порядка 2 %. При этом, можно обратить внимание на следующие закономерности.
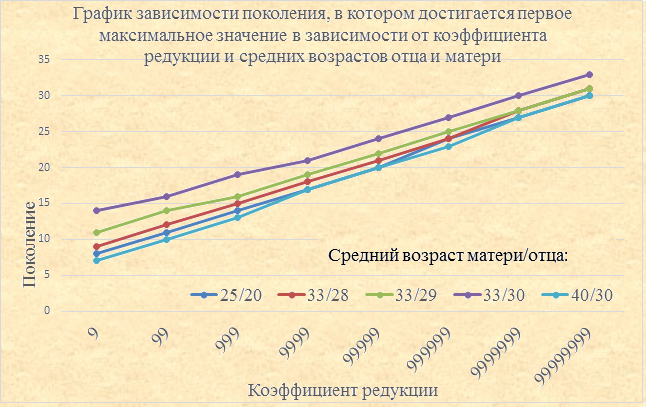
Посмотрим в каком поколении достигается максимальное число предков для разных коэффициентов редукции и средних возрастов отца и матери. График 6
Так, для коэффициента редукции равного 33 333 332, возраста отца равного 33 годам и матери - 28 годам (график красного цвета) максимум достигается в 29 поколении. Из графика видны следующие закономерности.
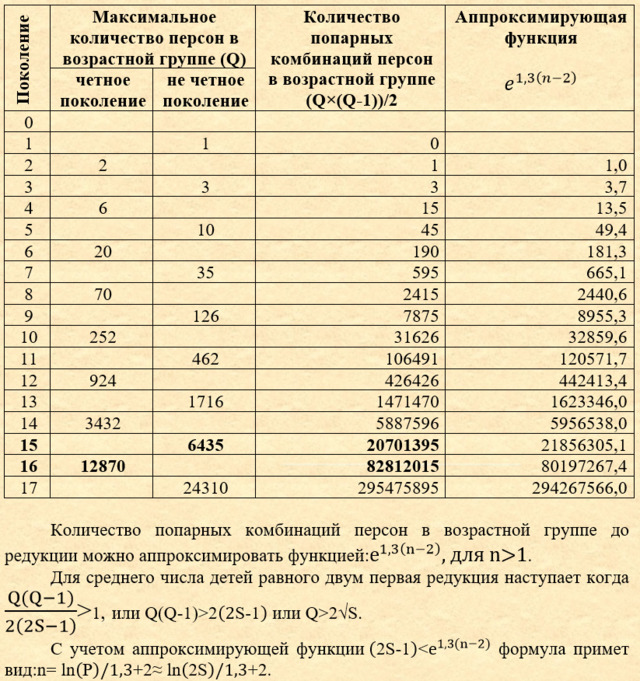
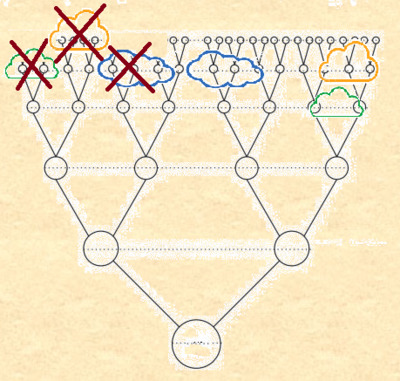
Для вычисления поколения в котором достигается первое максимальное значение можно воспользоваться примерной формулой: (((0,0036×(41-Vо)+0,085)×(Vо-Vм)-0,085)×lg(P+1)+0,9)×Vо/(Vо-Vм)-0,085, рассчитанной для возраста отца от 25 до 40 лет, матери от 20 до 37 лет и разнице в возрасте родителей от 3 до 8 лет. Например, для вышеуказанных характеристик: (((0,0036×(41-33)+0,085)×(33-28)-0,085)×lg(33333332+1)+0,9)×33/(33-28)-0,085=29,88. Получилась ошибка в 1 поколение по сравнению с теоретическим расчетом. Найдем поколение родословного дерева, до которого обязательно произойдет редукция. Первая редукция произойдет, когда количество попарных комбинаций персон в возрастной группе достигнет значения коэффициента редукции (P≈33 333 332). Очевидно это произойдет в самой многочисленной возрастной группе. Как следует из треугольника Паскаля это значение находится в центре строки. Любое m-е число (при нумерации с 0) треугольника паскаля в строке n можно вычислить по формуле:. Тогда максимальное значение в треугольнике паскаля для нечетных строк (при m=(n-1)/2) можно вычислить по формуле: Ниже приведена таблица с рассчитанными максимальными значениями. Таблица 6 Например, для коэффициента редукции равного P=33 333 332: Q>2√S=2√16666666=8165, что соответствует в треугольнике Паскаля 15-16 поколению. Или в соответствии с аппроксимирующей функцией: n≈ ln(P)/1,3+2=ln(33333332)/1,3+2=15,3
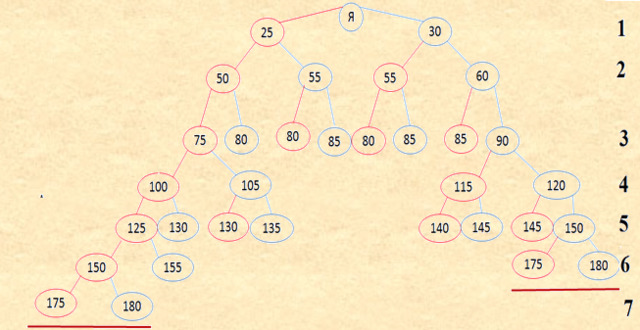
Найдем первое поколение, в котором предки одной возрастной группы общества (с учетом пола) будут присутствовать в нескольких поколениях восходящего родословного дерева. Суть задачи можно понять из следующего примера, на котором отображено дерево со средним возрастом отца равным 30 лет и матери-25 лет. Схема 9 Как видно из схемы в 7 поколении появились возрастные группы аналогичные возрастным группам 6 поколения.
Заметим, что первая редукция за счет пересечения предков между поколениями возможна только в следующем поколении, поскольку мы из дерева исключаем предков из старшего поколения, при их совпадении с предками из более ранних поколений. Вернемся к Закону трех поколений. Посмотрим, как будут меняться границы среднего возраста поколений при наличии редукции и среднего возраста матери равного Vм=28 годам, а отца Vо=33 годам. С увеличением числа поколений нижняя граница среднего возраста поколения стремится к верхнему значению (возрасту отца). И это объяснимо. Схема 10 При наличии редукции только внутри одного поколения (на схеме отмечено синим цветом), редукция происходит в средних возрастных группах, поскольку там наибольшее число предков (Схема 6), а в крайних возрастных группах не происходит по причине их малочисленности. Но при учете редукции для разных поколений (на схеме отмечено зеленым и желтым цветом), мы видели (Таблица 5), что редукция происходит за счет совпадений старших возрастных групп предыдущих поколений и младших возрастных групп текущего поколения. Таким образом, из текущего поколения, за счет редукции, исключаются персоны наиболее молодые (младшая возрастная группа), тем самым нижняя граница среднего возраста поколения увеличивается и стремиться к верхней границе (среднему возрасту отца). Следовательно, раскрывая смысл Закона трех поколений следует говорить о его справедливости без учета Закона убывания предков.
Другими словами, если средний возраст поколения составляет 28-33 года без учета редукции, то с учетом редукции средний возраст поколения будет стремиться к 32-33 годам. |
Назад:
Функция числа предков с учетом редукции
Вперед:



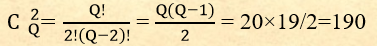 ), но совпали из них только две. Тогда коэффициент редукции будет равен Р=190/2=95, т.е. на 95 различных комбинаций приходится два совпадения. Такие расчеты можно делать на основе большого дерева, при небольшом числе предков вероятны значительные отклонения.
), но совпали из них только две. Тогда коэффициент редукции будет равен Р=190/2=95, т.е. на 95 различных комбинаций приходится два совпадения. Такие расчеты можно делать на основе большого дерева, при небольшом числе предков вероятны значительные отклонения.