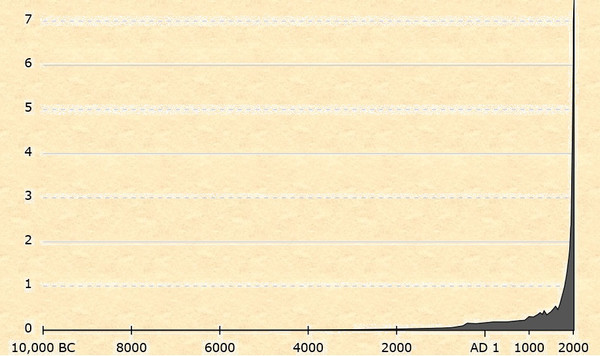
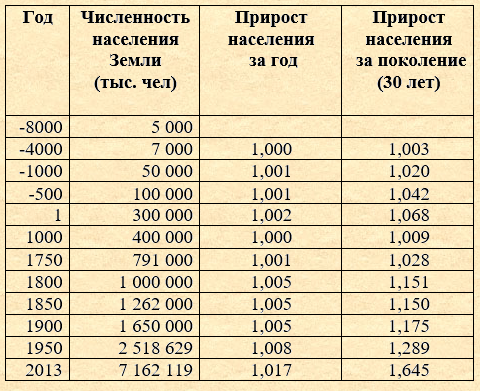
|
Подготовительные исследования
Заметим, что редукция может происходить как среди предков одного поколения, так и среди предков нескольких поколений. Это важно для дальнейших расчетов.
Будем полагать условия (численность, число детей, средний возраст родителей, местность, сословие, вероисповедание, национальность, отсутствие миграции, плотность населения, мобильность, развитие медицины, войны, смертность, благосостояние и т.д.) постоянными (демографическая модель стационарного населения со средним числом детей равным 2, которая предполагает равенство рождений и смертей, т.е. естественный прирост, равный нулю, а численность населения постоянную. Такая модель не имеет аналогов в обществе, однако она играет значительную практическую роль в прогнозировании), что примерно соответствует общим тенденциям роста населения Земли (https://ru.wikipedia.org/wiki/Население_Земли, График 1) на протяжении некоторого времени с нулевым приростом населения. Будем рассматривать круг людей, у которых могут быть совместные дети.
При этом, каждый может представлять свои условия для данной популяции и частично или полностью изолированных от особей других таких же групп), например, племя, село, волость, губерния, страна, Земля, а внутри территории сословие, вероисповедание, национальность и т.д. И поскольку каждое дерево носит индивидуальный характер, будем рассматривать средние значения, как и в Законе трех поколений. И чем условия будут менее постоянными, тем значительней будет отклонение от среднего значения, но общие тенденции сохраняться.
Учитывая данные ограничения, можно считать, что данное исследование в большой степени носит методологическую направленность и применение его на практике затруднительно.
Общие тенденции роста населения Земли представлены на графике ниже:
График 1
Как видно из таблицы ниже, длительное время прирост населения был очень небольшим:
Таблица 1
Следовательно, среднее число детей можно принять равным 2, только в двух последних поколениях это значение достигло 3.
Данное исследование будет проводиться исходя из демографической модели стационарного населения со средним числом детей равным 2 с некоторыми отступлениями.
Рассмотрим восходящее родословное дерево с указанием средних возрастов матери и отца. Для определения средних возрастов матери и отца можно воспользоваться статистическими исследованиями в сети Интернет.
Эти средние значения относятся к любым персонам, их родителям, родителям родителей и т.д.
Очевидно, что в перспективе все предки общества (рассматриваемой группы) в соответствии с Законом удвоения предков попадут в восходящее родословное дерево (в дальнейшем под «перспективой» будет пониматься время, когда все предки общества (рассматриваемой группы) попадут в восходящее родословное дерево), поэтому значения характеристик в восходящем родословном обществе будут равны значениям характеристик общества. Например, в обществе (группе людей) все мужчины 31 и 35 лет (в среднем 33 года), если в родословное дерево попадут все мужчины, то среднее значение останется 33 года, а если 50%, то среднее значение также будет стремиться к 33 годам, поскольку половина будет 35-летних мужчин, а вторая половина-31 летних.
|
Закон соответствия значений характеристик общества и родословного дерева. Родословное дерево (восходящее и нисходящее) является выборкой из общества, поэтому значения характеристик родословного дерева соответствуют значениям характеристик общества (рассматриваемой группы людей), а в перспективе равны между собой, в том числе средний возраст отца и средний возраст матери, число кровных браков, число повторных браков, среднее число детей и прочее.
|
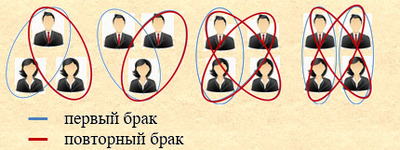
Схематично родословные деревья, являющиеся выборкой из поколений общества можно отобразить так:
Если рассматривать несколько восходящих деревьев (на схеме выше отмечены зеленым и синим цветом), то в части их пересечений можно утверждать следующее.
|
Закон пересечения восходящих деревьев. Восходящие деревья нескольких персон (в общем случае) состоят из нескольких частей: непересекающихся (ближайшие поколения), частично пересекающихся (далекие поколения) и полностью совпадающих (очень далекие поколения). При этом, один и тот же предок может находиться с исследуемыми персонами в разной степени родства.
|
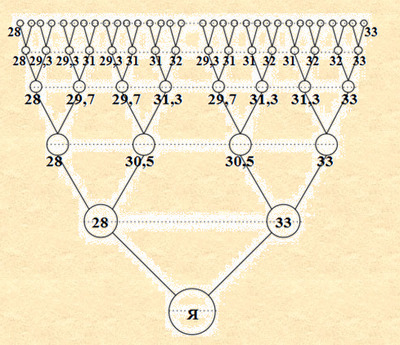
Закон соответствия значений характеристик общества и родословного дерева. Родословное дерево (восходящее и нисходящее) является выборкой из общества, поэтому значения характеристик родословного дерева соответствуют значениям характеристик общества (рассматриваемой группы людей), а в перспективе равны между собой, в том числе средний возраст отца и средний возраст матери, число кровных браков, число повторных браков, среднее число детей и прочее.
Из Закона трех поколений вытекает, что средний возраст матери равен 28 годам (Vм), а средний возраст отца-33 годам (Vо), которые являются средними значениями как для общества, так и для родословного дерева. Именно этих значений мы и будем придерживаться. Любые другие средние значения приведут к нарушению Закона трех поколений.
Для конкретных деревьев средние величины могут быть иными.
Тогда восходящее родословное дерево с возрастами предков можно изобразить следующим образом:
Схема 2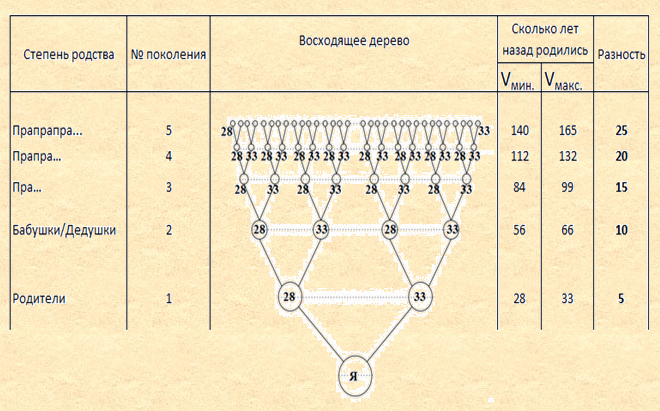
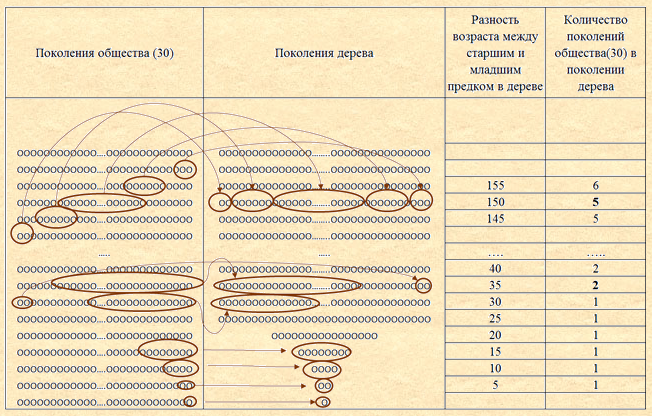
Где Vмин.-разница в возрасте с самым младшим предком, Vмакс.-разница в возрасте с самым старшим предком. Из схемы видно, что с каждым поколением разность в возрасте между младшим и старшим предком увеличивается на 5 лет и равна(n×(Vо-Vм)), где n – номер поколения в восходящем родословном дереве.
Таким образом, в 30 поколении разница между самым старшим предком и самым младшим будет равняться 150 лет, что составит более 2 поколений общества исходя из средней продолжительности жизни 60-70 лет. Т.е. в 30 поколение попадут люди, которые жили не только в определенное время, но и до, и после них. При этом численность их пока не известна из-за редукции.
Для лучшего понимания следует ввести следующую терминологию:
- поколение общества (период времени) – общность членов некоторого общества по времени жизни;
- поколение дерева – родственники одной степени родства.
Тогда, поколение общества (1) – люди, жившие в одном году, поколение общества (75) - все люди, жившие на протяжении 75 лет в одно время, поколение общества (30) - все люди, жившие на протяжении 30 лет в одно время (репродуктивный возраст).
Взаимосвязь между поколениями общества и поколениями дерева можно представить в виде следующей схемы:
Схема 3
Рассматриваем схему снизу-вверх. Сначала предки из одного поколения общества попадают в одно поколение дерева, но с увеличением поколений разность в возрасте между предками увеличивается и наступает момент, когда в одно поколение дерева попадают предки из разных поколений общества.
Люди, жившие в одно время, могут находятся в разных поколениях дерева, и, наоборот, люди, проживавшие в разное время, могут находиться в одном поколении дерева.
Например, одна из Ваших пра…прабабушек из 30 поколения, которая жила 1000 лет назад могла иметь мужа, который к этому времени уже умер (или еще не родился), но тем не менее все они находятся в 30 поколении.
Т.е. в одном поколении родословного дерева могут находиться персоны, проживавшие в разное время и с увеличением числа предков - это время увеличивается.
|
Закон о связи поколений дерева и поколений общества. В одном поколении родословного дерева (восходящего и нисходящего) могут находиться персоны из разных поколений общества и, наоборот, персоны из одного поколения общества могут находиться в разных поколениях дерева (восходящего и нисходящего).
В поколении n восходящего родословного дерева присутствуют
люди из (n×(Vо-Vм)/V) поколений общества (без учета редукции и пола), где
n – номер поколения в восходящем родословном дереве,
(Vо-Vм) -разность между средними значениями возраста предков (отца и матери), V-период поколения общества.
Для восходящего родословного дерева закон начинает действовать с поколения общества n×(Vо-Vм)/V>1.
В нисходящем дереве закон может работать в любом поколении дерева, когда разность в возрасте между двумя персонами одного поколения дерева более V лет или разность в возрасте между двумя персонами разных поколений дерева менее V лет.
|
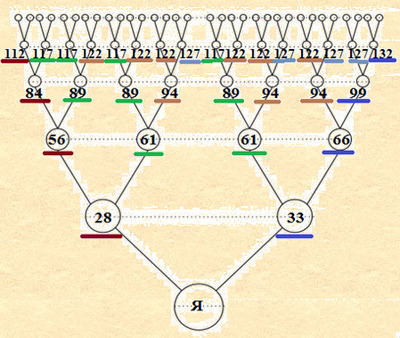
Тогда наличие редукции можно объяснить с помощью следующих рассуждений.
При отсутствии редукции, в 33 поколении у каждого человека должно быть более 8 миллиардов предков. С другой стороны, (принимая с запасом за среднюю продолжительность поколения общества в 22 года, а разницу между средним возрастом отца и матери в 10 лет) в 33 поколении могут присутствовать персоны из (n× (Vо-Vм)/V)=33×10/22=15 поколений. Предполагая, что население Земли в тот период составляло 0,5 миллиарда человек, в 33 поколении могло оказаться не более 7,5 (15×0,5) миллиардов человек, что меньше 8 (233)миллиардов человек.
Поскольку восходящее родословное дерево является выборкой из общества, то количество кровных браков в восходящем родословном дереве зависит от количества кровных браков, заключаемых в обществе, которые в свою очередь зависят от ряда факторов, например, от религиозных ограничений, вероисповедания, от сословий, миграции, от рода деятельности, государственных законов, числа детей в семье, национальности, возраста родителей, местности и численности населения, где проживали предки, плотности населения, благосостояния, медицины, войн, смертности и прочее. При этом, один и тот же фактор может влиять как в одну, так и в другую сторону. Например, с одной стороны религия может запрещать браки между близкими родственниками, тем самым отодвигая возможную редукцию предков, с другой стороны запрещает браки между разными религиями, тем самым сокращает круг возможных браков способствуя скорейшей редукции предков. При этом все эти факторы, в итоге сводятся к следующим численным характеристикам, от которых зависит редукция предков.
Во-первых, от численности населения. Будем полагать, что браки заключаются случайным образом. Тогда, например, если Ваши предки проживали в небольшой обособленной деревне, то вероятность родственных браков высока. Если Ваши предки жили в небольшом городе, то несколько поколений могут обойтись без родственных браков, ну а если Ваши предки имели возможность передвигаться по всему миру, то родственных браков в ближайших поколениях не будет. Но как показывают расчеты, даже в последнем случае, редукция наступит не позднее 16 поколения.
Но если говорить более точно, то возможность родственных браков зависит не от общей численности населения, а от численности возрастной группы, среди которой могут заключаться браки. При этом, численность возрастных групп зависит от числа ежегодно рождающихся детей (общая численность населения (мужчин/ женщин) деленная на их средний возраст жизни - это во-вторых), в свою очередь имеющих потомков.
Численность населения в возрастной группе зависит от продолжительности периода времени, который равен разнице в возрасте родителей - это в-третьих (например, в пятилетний период попадет одно число персон, а в 10-летний – в два раза больше). И как видно из Схемы 3, чем больше эта разность, тем больший период времени входит в одно поколение восходящего родословного дерева.
В-четвертых, от среднего числа детей в семье. Например, если в восходящее родословное дерево попало 6 человек, среди которых две тройки братьев/сестер (2х3=6), то в поколении родителей произойдет уменьшение на 4‑х персон одного пола (останется 2‑е родителей), а если три пары братьев/сестер (3х2=6), то в поколении родителей произойдет уменьшение на 3-х персон одного пола (останется 3-е родителей).
В-пятых, редукция зависит от числа предков в рассматриваемом поколении. Очевидно, что чем больше предков в поколении восходящего родословного дерева (чем старше поколение), тем больше вероятность наступления редукции, повторения предков.
Предположим, что в восходящее родословное дерево попало все население, тогда в нем обязательно будут братья/сестры и как следствие в поколении родителей - редукция предков, а если в первые поколения восходящего дерева попало всего несколько человек из популяции, то вероятность того, что редукция наступит в поколении родителей не велика.
В-шестых, лица одной возрастной группы общества распределяются по поколениям восходящего родословного дерева в зависимости от среднего возраста родителей (отца и матери). Например, если средний возраст родителей 20 лет, то за столетие будет 5 поколений, а если 50 лет, то – только 2 поколения.
Несмотря на то, что параметры от которых зависит редукция определены, конкретные значения рассчитаны быть не могут, поскольку это вероятностные величины. Это как, например, Вы подбрасываете монету 100 раз, а сказать сколько раз выпадет «орел» не можете, но знаете, что эта величина будет близкой к 50%.
Также повторение предков (редукция) не может происходить среди персон разного пола, поэтому все расчеты должны выполняться среди предков одного пола.
Как уже говорилось, редукция наступает, когда в восходящем родословном дереве несколько раз появляется одна и та же персона. Одной и той же персоной могут быть предки, у которых совпадает средний возраст и пол.
Посмотрим, как распределяется средний возраст одного поколения дерева, который лежит в пределах от 28 до 33 и зависит от числа предков мужского и женского пола.
Из схемы ниже, видно, что минимальный средний возраст поколения соответствует крайней левой ветви со средним возрастом матери в 28 лет. Максимальный средний возраст поколения соответствует крайней правой ветви со средним возрастом отца в 33 года. В промежуточных ветвях средний возраст поколения лежит в пределах от 28 до 33 лет, что соответствует Закону трех поколений.
Схема 4
Также, можно посчитать сколько лет назад (в среднем) жили предки среднестатистического «Я»:
Схема 5
Следует заметить, что средний возраст рождения предков может совпадать не только для одного поколения, как на схеме, но и в нескольких поколениях.
Из представленных схем видны следующие возрастные группы (с периодом равным разнице в возрасте родителей) для одного пола по поколениям:
Таблица 2
Видно, что число предков в возрастных группах представляет из себя треугольник Паскаля, известный из средней школы. В этом треугольнике на вершине и побокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел: Cni = C(n-1)(i-1) + C(n-1)(i), где n-номер поколения, i-номер возрастной группы (от 2 до n-1). Строки треугольника симметричны относительно вертикальной оси.
Чем больше общая численность населения, тем больше численность предков в возрастных группах.
Если бы не было редукции предков, то число предков по возрастным группам (в среднем) распределялось бы в соответствии с треугольником Паскаля:
Схема 6
При этом, понятно, что количество возрастных групп (с периодом равным разнице в возрасте между родителями) и число предков в возрастных группах не зависят от среднего возраста матери и отца, что будет важным в дальнейшем.
Надо заметить, что в представленном треугольнике в возрастных группах присутствуют предки мужского и женского пола, количество которых в возрастных группах также соответствует треугольнику Паскаля:
Схема 7
|
Закон о числе предков в возрастных группах без учета редукции восходящего родословного дерева. Среднее число предков, без учета редукции, в восходящем родословном дереве по возрастным группам (по всем персонам и по персонам мужского и женского пола в отдельности) каждого поколения распределено в соответствии с треугольником Паскаля.
Среднее число предков в возрастной группе (с периодом равным разнице в возрасте родителей) восходящего родословного дерева по персонам мужского и женского пола в отдельности смещено относительно всех персон на одно поколение и определяется формулой:
Qni=Q=Q(n-1)(i-1)+Q(n-1)(i), где
n – номер поколения (для n>1),
i -номер возрастной группы,
Q(n-1)(i-1), Q(n-1)(i) - число предков (основанное на треугольнике Паскаля) с учетом редукции в соответствующих возрастных группах предыдущего поколения
|
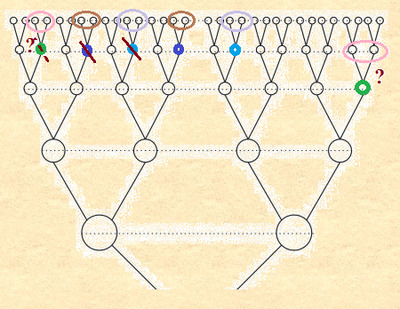
Зачастую, когда речь идет о редукции предков, можно встретить примерно такую фразу: «Отто Форст Баттаглиа привел сравнительную таблицу количества теоретических предков и реальных для исторических лиц, у которых известны все предки. По этой таблице в XI поколении, где число теоретических предков 1024, у испанского короля Альфонса XIII их 111 (меньше всего), у графа Генриха Парижского (Генрих VI) – 181, наибольшее количество предков в этом поколении – 588 – у бельгийского короля Леопольда III.».
При этом, совершенно не понятно число теоретических предков указано для конкретного поколения с учетом возможных совпадений предков в других поколениях или без учета таковых?
Так, например, в X поколении у Вас 300 предков, в XI поколении 10 предков повторились, таким образом в XI поколении не 600, а 590 предков. При этом, часть из них может совпасть с персонами из предыдущих (до XI) поколений. Но, несмотря на это, в XI поколении 590 предков.
Рассмотрим ситуацию с помощью следующей схемы.
Схема 8
|
|
Предки, обозначенные синим цветом, повторились и исключены из дерева. Предки, обозначенные зеленым цветом тоже повторились, но если одного из них удалить (какого ?), то в одном из поколений не будет предка, хотя он занимает свое место в поколении дерева.
Предки обозначенные зеленым цветом жили в одно время, поскольку это одна и та же персона.
|
Чтобы избежать данной коллизии, можно говорить об общем числе предков до текущего поколения (см. Закон об общем числе предков ниже), но мы из дерева будем исключать предков из старшего поколения, при их совпадении с предками из более ранних поколений.
|
Закон о соотношении числа мужчин и женщин. В каждом поколении и во всем дереве в целом число предков мужского и женского пола без учета редукции составляет по 50 %.
В перспективе фактическое число предков женского пола в родословном дереве может превышать число предков мужского пола, с учетом редукции, пропорционально числу повторных браков, примерно на 20 -30%.
Для конкретных периодов и стран могут быть исключения.
|
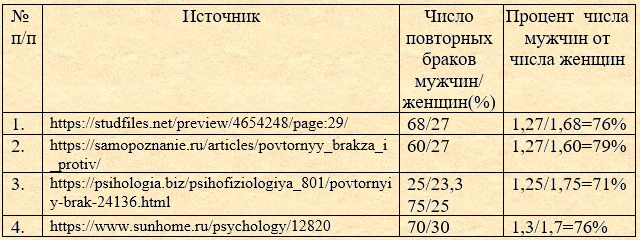
Возможность не равного числа предков мужского и женского пола вызвана повторными браками, наличием неполнородных братьев и сестер и как следствие возможностью редукции только для одного родителя.
В первых поколениях это превышение невелико, в связи с незначительной редукцией или ее отсутствием.
Статистические данные о числе повторных браков приведены в таблице.
Таблица 3
В зависимости от различных схем повторных браков (с персоной, впервые вступающей брак или тоже повторно) этот процент может несколько отличаться.Учитывая Закон соответствия значений характеристик общества и родословного дерева, можно утверждать, что данное соотношение распространяется и на генеалогические деревья.
|
